Stability

Power system stability is the ability of a Power System (PS) under a certain operating condition to re-establish an equilibrium operating state after being subjected to a physical disturbance. Stability has been recognized as an important issue for operational security since the 1920s. Many large-scale blackouts caused by power system instability have illustrated the importance of this phenomenon.

Normally, two types of stability studies are performed (a more detailed classification can be found in this paper). The recovery from a sudden and severe disturbance is called transient stability, and its solution is generally obtained in the time domain. Another study is called dynamic stability, used to describe the system’s response to small disturbances over a long time, which can be solved either in the frequency domain or in the time domain.

Information

In PSP-UFU, dynamic stability is treated as an extension of transient stability, where the effects of small time constants must be ignored.

The model for representing the PS in a transient stability study is built using a system of differential-algebraic equations (DAEs), in which the initial state is considered stable and obtained from a power flow study. The equations are solved using a numerical integration method, and the power system’s response is then observed.

If the solution in the time domain, after a disturbance, drives one or more system parameters to physically impossible values or if the solution of the differential equations does not converge in iterative processes, the system is said to be unstable. Conversely, if the system element state variables oscillate after a disturbance and settle at a new operating point, even if different from the initial values, the system is considered stable.

Running the stability study in PSP-UFU

After building the single-line diagram in the power editor, as well as the controls of the synchronous machines, the stability analysis is performed in the Simulation menu by clicking the Run Stability button. Clicking on the lower part of the "Run Stability" button displays a dropdown menu with the option Stability Event List.

When running the stability calculation, a box showing the status of the simulation process will be displayed, first indicating the initialization of the study and then the calculated simulation time.

Clicking on the stability event list will display a window with the description of the inserted stability events.

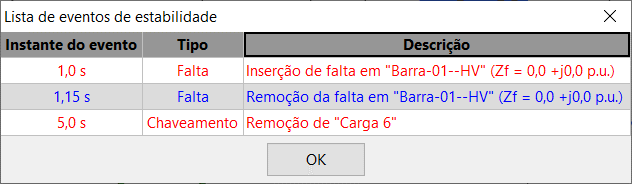
Inserting a stability event

The most common disturbances applied in transient stability studies are faults and switchings. Such operations are easily performed in PSP-UFU:

• Faults: Three-phase short circuits can be inserted at system buses by including the fault impedance in the bus admittance matrix, in the same way as a shunt element. This value is defined by the user, and in the case of a bolted fault, a non-zero value but sufficiently close to zero is applied so that the bus voltage is driven to zero during the disturbance.

• Branch switching: As with faults, branch switching is performed by altering the admittance matrix, removing or inserting the parameters of the element to be switched. Each power element has a "Switching" or "Stability" button, where the removal and/or insertion times of the component can be entered.

• Machine switching: The removal of a synchronous machine is carried out by eliminating its participation in the current vector, as well as the removal of its fictitious admittance.
  As with power elements, synchronous machines have a "Switching" button, where the removal and/or insertion times of the component can be entered.

  Warning!

  Even if removed from the bus, the synchronous machines parameters continue to be calculated with zero stator current, potentially providing results upon reconnection.

Tip

Events in control systems can be easily introduced with the math expression block. In this case, such events will not be displayed in the stability event list.

Common errors when running the stability study

The following are the most common errors related to the stability study.

The following error message is displayed: "Unable to build the admittance matrix"

This error message is displayed when it is not possible to build the bus admittance matrix. The following situations may cause this error:

• Circuit parameters are incorrect. If parameters far from typical values of electrical elements are entered, the power flow calculation may diverge. Check if the data was entered correctly.
• A bus is isolated. This error is quite common and can occur when inserting a bus without connecting it to the system or removing branch elements that connect a bus to the system. The solution is to eliminate this bus from the diagram.
• An element has parameters very different from the others. If one of the inserted elements has an impedance value very different from the others, such as a line with very high impedance or a very small load, it may lead to divergence of the numerical method. In this case, reconsider the need to represent these elements in the circuit and switch between available numerical solution methods.

The following error message is displayed: "Error initializing saturation values of..."

This error message is displayed when it is not possible to calculate the saturation factors of the synchronous machine. The following situations may cause this error:

• The saturation factor is less than 1.2. This value must be greater than 1.2, otherwise it will cause simulation errors. If not specified, the machine’s saturation is not considered in the calculations.
• Synchronous machine parameters are incorrect. If parameters far from typical values of synchronous machines are entered, the calculation of saturation factors may diverge. Check if the data was entered correctly.

The following error message is displayed: "Error initializing the AVR / speed governor..."

This error message is displayed when it is not possible to initialize the control system of a synchronous machine. The following situations may cause this error:

• The control system is empty. If the AVR and/or speed governor is enabled and the control has not been inserted, this error may occur. Insert the machine’s control or uncheck the AVR and/or speed governor usage option.
• The control system does not have at least one input and one output. The control system must have at least one input and one output, otherwise it will present an execution error.
• The integration step is too small. If the integration step is too small, calculations will produce errors and diverge. Increase the integration step in the simulation settings.

The following error message is displayed: "Unable to solve system machines"

This error message is displayed when it is not possible to solve the DAEs of synchronous machines inserted in the system. The following situations may cause this error:

• Synchronous machine parameters are incorrect. If parameters far from typical values of synchronous machines are entered, the calculation of the DAEs may become impossible. Check if the data was entered correctly.
• The integration step is too small. If the integration step is too small, calculations will produce errors and diverge. Increase the integration step in the simulation settings.
• Circuit parameters are incorrect. If parameters far from typical values of electrical elements are entered, the power flow calculation may diverge. Check if the data was entered correctly.
• A bus is isolated. This error is quite common and can occur when inserting a bus without connecting it to the system or removing branch elements that connect a bus to the system. The solution is to eliminate this bus from the diagram.
• An element has parameters very different from the others. If one of the inserted elements has an impedance value very different from the others, such as a line with very high impedance or a very small load, it may lead to divergence of the numerical method. In this case, reconsider the need to represent these elements in the circuit and switch between available numerical solution methods.

The following error message is displayed: "Error initializing motor slip..."

This error message is displayed when it is not possible to calculate the initial slip value of the induction motor. The following situations may cause this error:

• Motor stability parameters are incorrect. If parameters far from typical values of induction motors are entered, the calculation of slip may become impossible. Check if the data was entered correctly.

Stability tool structure

Power system stability is a dynamic problem and requires more elaborate models of power elements compared to those presented in other studies. These models are described individually, with emphasis on synchronous machines, ZIP loads, and induction motors.

The representation of other power system components: transmission lines, transformers, and shunt elements (except ZIP loads), which form the balanced transmission or distribution network, is carried out using the same models from power flow.

Dynamic models for time-domain analysis are in the form of a system of differential-algebraic equations (DAEs), described as follows:

$$\dfrac{dx}{dt}= f(x,y,u)\\ g = f(x,y)$$

Where:

• $x$ are the state variables
• $y$ are the algebraic variables
• $u$ are the input variables

The input variables are provided by the user and remain constant throughout the calculation process. For the stability problem, the initial algebraic variables correspond to bus voltages and angles calculated in the power flow. The initial state variables are estimated after the power flow convergence (initialization of dynamic elements).

Next, the structure of the stability module implemented in PSP-UFU is presented in the form of flowcharts. The flowchart below shows the general structure of the stability tool.

The initialization of the power grid and dynamic elements, as well as the iterative process for solving the DAEs, are shown in the two flowcharts below.

Numerical integration

To solve machine differential equations, a numerical integration method is required. Such methods are classified into two groups: explicit methods and implicit methods. Explicit methods, due to their formulation, directly calculate the system state at a later time instant, while implicit methods involve both current and future states in their equations, thus requiring an iterative process.

The time constants present in the stability study vary greatly in their value (they can range from $10^{-3}~s$ to $10~s$). This makes the synchronous machine’s system of differential equations a stiff system (stiff equation). If the numerical stability analysis of both the stiff differential equations and the integration method shows the same behavior, the method is called absolutely stable, or A-stable.

Explicit numerical integration methods, such as the fourth-order Runge-Kutta, cannot be A-stable and therefore usually perform poorly in problems with stiff differential equations. On the other hand, implicit methods can be A-stable. A suitable implicit method for solving the dynamic behavior of power systems is the Implicit Trapezoidal method, as it has the following advantages:

• It is numerically stable (A-stable);
• It is very fast;
• It has good accuracy (depending only on the integration step used).

This method was implemented in PSP-UFU both for solving the differential equations of the synchronous machine and in the transfer functions of the control system. Its formulation is given by the following expression:

$$y_{n+1}=y_n + 0.5 h \left(y_{n+1}' + y_{n}' \right)$$

Where:

• $h$ is the integration step
• $y_n$ is the state value at the previous step (instant $t_n$)
• $y_{n+1}$ is the state value at the current step (instant $t_{n+1}$)
• $y_{n}'$ is the differential equation at the previous step
• $y_{n+1}'$ is the differential equation at the current step

It can be seen in this equation that the method is implicit because the $n+1$ term appears on both sides of the equation, which is why an iterative process is necessary for its solution.

References

1. MILANO, F. Power System Modelling and Scripting. London: Springer, 2010. doi: https://doi.org/10.1007/978-3-642-13669-6
2. KUNDUR, P.; et al. Definition and classification of power system stability. IEEE Transactions Power Systems, v. 19, n. 2, May 2004, p. 1387-1401. doi: https://doi.org/10.1109/TPWRS.2004.825981
3. ARRILLAGA, J.; WATSON, N. R. Computer Modelling of Electrical Power Systems. Wiley & Sons, New York, 2001. doi: https://doi.org/10.1002/9781118878286
4. PARK, R. H. Two-reactions Theory of Synchronous Machine. Generalized Method of Analysis – Part I. AIEE Transactions, v. 48, n. 3, Jul 1929. doi: https://doi.org/10.1109/T-AIEE.1929.5055275
5. ANDERSON, P. M.; FOUAD, A. A. Power System Control and Stability. Wiley-IEEE Press, New York, 2002. doi: https://doi.org/10.1109/9780470545577
6. SAUER, P. W.; PAI, M. A. Power System Dynamics and Stability. Prentice Hall, Upper Saddle River, 1998.
7. KUNDUR, P. Power System Stability and Control. McGraw-Hill, New York, 1994.
8. DOMMEL, H. W.; SATO, N. Fast Transient Stability Solutions. IEEE Transactions on Power Apparatus and Systems, v. PAS-91, n. 4, Jul 1972, p. 1643-1650. doi: https://doi.org/10.1109/TPAS.1972.293341