Estabilidade

Estabilidade de sistemas de potência é a habilidade de um Sistema Elétrico de Potência (SEP), para uma certa condição de operação, de reestabelecer um estado de operação de equilíbrio após ser submetido a um distúrbio físico. A estabilidade é reconhecida como um importante problema para a segurança da operação desde a década de 1920. Muitos blackouts de grande porte causados pela instabilidade do SEP têm ilustrado a importância desse fenômeno.

Normalmente são realizados dois tipos de estudos de estabilidade (uma classificação mais aprofundada pode ser observada nesse artigo). A recuperação de uma rápida e brusca perturbação é chamada de estabilidade transitória, e sua solução é geralmente obtida no domínio do tempo. Outro estudo é denominado estabilidade dinâmica, utilizado para descrever a resposta do sistema frente a pequenas perturbações ao longo de muito tempo, o qual pode ser resolvido tanto no domínio da frequência quanto no domínio do tempo.

Informação

No PSP-UFU, a estabilidade dinâmica é tratada como uma extensão da estabilidade transitória, em que os efeitos de pequenas constantes de tempo devem ser ignorados.

O modelo para representação do SEP em um estudo de estabilidade transitória é feito por meio do sistema de equações algébrico-diferenciais (EADs), em que o estado inicial é considerado estável e originado de um estudo de fluxo de carga. A solução das equações se dá por meio de um método de integração numérica e, então, é observada a resposta do sistema de potência.

Caso a solução no domínio do tempo, após alguma perturbação, leve um ou mais parâmetros do sistema a valores fisicamente impossíveis ou, até mesmo, a solução das equações diferenciais não obtenha convergência em processos iterativos, o sistema é dito instável. Em contrapartida, caso as variáveis de estado dos elementos do sistema oscilem após uma perturbação e se estabeleçam em um novo ponto de operação, mesmo que distinto dos valores iniciais, o sistema é considerado estável.

Execução do estudo de estabilidade no PSP-UFU

Após a construção do diagrama unifilar no editor de potência, assim como os controles das máquinas síncronas, a execução da estabilidade é realizada no menu Simulação clicando no ícone do botão Executar Estabilidade. Ao clicar na parte inferior do botão "Executar Estabilidade" será exibido um menu suspenso com a opção Lista de eventos de estabilidade.

Ao executar o cálculo de estabilidade, uma caixa com o status do processo de simulação será exibida, indicando primeiramente a inicialização do estudo e posteriormente o tempo de simulação calculado.

Ao clicar na lista de eventos de estabilidade, será exibida uma janela com a descrição dos eventos de estabilidade inseridos.

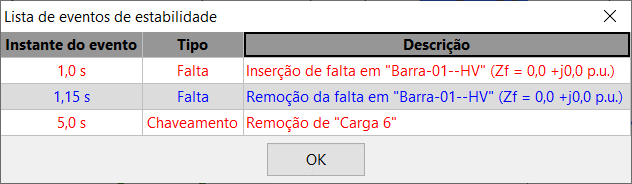
Inserindo um evento de estabilidade

Os distúrbios mais comuns aplicados em estudos de estabilidade transitória são faltas e chaveamentos. Tais operações são facilmente realizadas no PSP-UFU:

• Faltas: Curtos-circuitos trifásicos podem ser inseridos nos barramentos do sistema por meio da inclusão da impedância de falta na matriz admitância de barras da mesma maneira realizada em um elemento shunt. Tal valor é definido pelo usuário e caso seja um curto-circuito franco, um valor não nulo, mas suficientemente próximo de zero, é aplicado, de forma que a tensão no barramento é levada a zero durante o distúrbio.

• Chaveamento de ramo: Da mesma forma que as faltas, o chaveamento de ramos é realizado por meio da alteração na matriz admitância, removendo ou inserindo os parâmetros do elemento a ser chaveado. Cada elemento de potência possui um botão de "Chaveamento" ou "Estabilidade", em que pode ser inserido os tempos de remoção e/ou inserção do componente.

• Chaveamento de máquinas: A remoção de uma máquina síncrona é efetivada com a retirada de sua participação no vetor de correntes, além da remoção de sua admitância fictícia. Assim como os elementos de potência, as máquinas síncronas possui um botão "Chaveamento", em que pode ser inserido os tempos de remoção e/ou inserção do componente.

  Atenção!

  Mesmo que removida da barra, os parâmetros das máquinas síncronas continuam a ser calculados com a corrente do estator nula, podendo fornecer resultados em uma eventual reconexão.

Dica

Eventos nos sistemas de controle podem ser facilmente introduzidos com o bloco de expressão matemática. Nesse caso, tais eventos não serão exibidos na lista de eventos de estabilidade.

Erros comuns na execução do estudo de estabilidade

A seguir são apresentados os erros mais comuns relacionados ao estudo de estabilidade.

A seguinte mensagem de erro é exibida: "Não foi possível construir a matriz admitância"

Essa mensagem de erro é exibida quando não é possível construir a matriz admitância de barras. As seguintes situações podem ocasionar esse erro:

• Os parâmetros do circuito estão incorretos. Caso parâmetros muito fora dos valores padrão dos elementos elétricos sejam inseridos, o cálculo de fluxo de carga pode divergir. Verifique se os dados foram inseridos corretamente.
• Algum barramento está isolado. Esse erro é bastante comum e pode ocorrer ao inserir um barramento sem conectá-lo ao sistema ou ao remover os elementos de ramo que conectam uma barra ao sistema. A solução é eliminar essa barra do diagrama.
• Algum elemento possui parâmetros discrepantes dos demais. Caso um dos elementos inseridos possua um valor de impedância muito distinto dos demais, como por exemplo uma linha com impedância muito elevada ou uma carga muito pequena, pode levar à divergência do método numérico. Nesse caso, reconsidere a necessidade de representação desses elementos no circuito e alterne entre os métodos numéricos de solução disponíveis.

A seguinte mensagem de erro é exibida: "Erro ao inicializar os valores de saturação do..."

Essa mensagem de erro é exibida quando não é possível calcular os fatores de saturação da máquina síncrona. As seguintes situações podem ocasionar esse erro:

• O fator de saturação é menor que 1,2. Esse valor deve ser maior que 1,2, ou irá gerar erros na simulação. Caso não seja informado, a saturação da máquina não é considerada nos cálculos.
• Os parâmetros da máquina síncrona estão incorretos. Caso parâmetros muito fora dos valores padrão das máquinas síncronas sejam inseridos, o cálculo dos fatores de saturação pode divergir. Verifique se os dados foram inseridos corretamente.

A seguinte mensagem de erro é exibida: "Erro ao inicializar o AVR / regulador de velocidade..."

Essa mensagem de erro é exibida quando não é possível inicializar o sistema de controle de uma máquina síncrona. As seguintes situações podem ocasionar esse erro:

• O sistema de controle está vazio. Caso esteja habilitado o AVR e/ou o regulador de velocidade e o controle não foi inserido, esse erro pode ser acionado. Insira o controle da máquina ou desmarque a opção de utilização do AVR e/ou regulador de velocidade.
• O sistema de controle não possui ao menos uma entrada e uma saída. O sistema de controle deve ter ao menos uma entrada e uma saída, caso contrário apresentará erro de execução.
• O passo de integração está muito pequeno. Caso o passo de integração esteja muito pequeno, os cálculos gerarão erros e irão divergir. Reduza o passo de integração nas configurações de simulação.

A seguinte mensagem de erro é exibida: "Impossível resolver as máquinas do sistema"

Essa mensagem de erro é exibida quando não é possível resolver as EADs das máquinas síncronas inseridas no sistemas. As seguintes situações podem ocasionar esse erro:

• Os parâmetros da máquina síncrona estão incorretos. Caso parâmetros muito fora dos valores padrão das máquinas síncronas sejam inseridos, o cálculo das EADs pode se tornar impossível. Verifique se os dados foram inseridos corretamente.
• O passo de integração está muito pequeno. Caso o passo de integração esteja muito pequeno, os cálculos gerarão erros e irão divergir. Reduza o passo de integração nas configurações de simulação.
• Os parâmetros do circuito estão incorretos. Caso parâmetros muito fora dos valores padrão dos elementos elétricos sejam inseridos, o cálculo de fluxo de carga pode divergir. Verifique se os dados foram inseridos corretamente.
• Algum barramento está isolado. Esse erro é bastante comum e pode ocorrer ao inserir um barramento sem conectá-lo ao sistema ou ao remover os elementos de ramo que conectam uma barra ao sistema. A solução é eliminar essa barra do diagrama.
• Algum elemento possui parâmetros discrepantes dos demais. Caso um dos elementos inseridos possua um valor de impedância muito distinto dos demais, como por exemplo uma linha com impedância muito elevada ou uma carga muito pequena, pode levar à divergência do método numérico. Nesse caso, reconsidere a necessidade de representação desses elementos no circuito e alterne entre os métodos numéricos de solução disponíveis.

A seguinte mensagem de erro é exibida: "Erro ao inicializar o escorregamento do motor..."

Essa mensagem de erro é exibida quando não é possível calcular o valor de escorregamento inicial do motor de indução. As seguintes situações podem ocasionar esse erro:

• Os parâmetros de estabilidade do motor estão incorretos. Caso parâmetros muito fora dos valores padrão dos motores de indução sejam inseridos, o cálculo do escorregamento pode se tornar impossível. Verifique se os dados foram inseridos corretamente.

Estrutura da ferramenta de estabilidade

A estabilidade de um SEP é um problema dinâmico e necessita de modelos mais elaborados de elementos de potência comparados àqueles apresentados nos outros estudos. Esses modelos são descritos individualmente, com destaque às máquinas síncronas, cargas ZIP e motores de indução.

A representação dos demais componentes do sistema elétrico: linhas de transmissão, transformadores e elementos shunt (com exceção de cargas ZIP), que formam a rede de transmissão ou distribuição balanceada, é realizada utilizando os mesmos modelos do fluxo de carga.

Os modelos dinâmicos para a análise no domínio do tempo são na forma de um sistema de equações algébrico-diferenciais (EADs), descritas a seguir:

$$\dfrac{dx}{dt}= f(x,y,u)\\ g = f(x,y)$$

Em que:

• $x$ são as variáveis de estado
• $y$ são as variáveis de algébricas
• $u$ são as variáveis de entrada

As variáveis de entrada são inseridas pelo usuário e permanecem constantes durante todo o processo de cálculo. Para o problema de estabilidade, as variáveis algébricas iniciais correspondem às tensões e ângulos das barras calculadas no fluxo de carga. As variáveis de estado iniciais são estimadas após a convergência do fluxo de potência (inicialização dos elementos dinâmicos).

Na sequência é apresentado, na forma de fluxogramas, a estrutura do módulo de estabilidade implementado no PSP-UFU. O fluxograma abaixo mostra a estrutura geral da ferramenta de estabilidade.

A inicialização da rede elétrica e dos elementos dinâmicos, assim como o precesso iterativo para solução das EADs são apresentados nos dois fluxogramas conseguintes.

Integração numérica

Para resolver as equações diferenciais da máquina é necessário um método de integração numérica. Tais métodos são classificados em dois grupos: métodos explícitos e métodos implícitos. Os métodos explícitos, devido à sua formulação, calculam diretamente o estado do sistema em um instante de tempo posterior, enquanto métodos implícitos envolvem estados atuais e posteriores em suas equações, exigindo, portanto, um processo iterativo.

As constantes de tempo presentes no estudo de estabilidade têm uma grande variação em seu valor (podem variar de $10^{-3}~s$ a $10~s$). Isso torna o sistema de equações diferenciais da máquina síncrona como um sistema rígido (stiff equation). Caso a análise da estabilidade numérica tanto das equações diferenciais rígidas quanto do método de integração obtenham o mesmo comportamento, o método é chamado de absolutamente estável, ou A-estável.

Métodos de integração numérica explícitos, como por exemplo o Runge-Kutta de quarta ordem, não podem ser A-estáveis e, portanto, normalmente possuem comportamento ruim em problemas com equações diferenciais rígidas. Por outro lado, métodos implícitos podem ser A-estáveis. Um método implícito adequado para solução do comportamento dinâmico de sistemas elétricos é o Trapezoidal Implícito, por possuir as seguintes vantagens:

• É numericamente estável (A-estável);
• É bastante rápida;
• Possui boa precisão (dependendo somente do passo de integração utilizado).

Tal método foi implementado no PSP-UFU tanto para solução das equações diferenciais da máquina síncrona quanto nas funções transferência do sistema de controle. Sua formulação é dada pela seguinte expressão:

$$y_{n+1}=y_n + 0{,}5 h \left(y_{n+1}' + y_{n}' \right)$$

Em que:

• $h$ é o passo de integração
• $y_n$ é o valor do estado no passo anterior (instante $t_n$)
• $y_{n+1}$ é o valor do estado no passo atual (instante $t_{n+1}$)
• $y_{n}'$ é a equação diferencial no passo anterior
• $y_{n+1}'$ é a equação diferencial no passo atual

Nota-se nessa equação que o método é implícito devido ao termo $n+1$ aparecer em ambos os lados da equação, por isso é necessário um processo iterativo para sua solução.

Referências

1. MILANO, F. Power System Modelling and Scripting. London: Springer, 2010. doi: https://doi.org/10.1007/978-3-642-13669-6
2. KUNDUR, P.; et al. Definition and classification of power system stability. IEEE Transactions Power Systems, v. 19, n. 2, mai 2004, p. 1387-1401. doi: https://doi.org/10.1109/TPWRS.2004.825981
3. ARRILLAGA, J.; WATSON, N. R. Computer Modelling of Electrical Power Systems. Wiley & Sons, New York, 2001. doi: https://doi.org/10.1002/9781118878286
4. PARK, R. H. Two-reactions Theory of Synchronous Machine. Generalized Method of Analysis – Part I. AIEE Transactions, v. 48, n. 3, jul 1929. doi: https://doi.org/10.1109/T-AIEE.1929.5055275
5. ANDERSON, P. M.; FOUAD, A. A. Power System Control and Stability. Wiley-IEEE Press, New York, 2002. doi: https://doi.org/10.1109/9780470545577
6. SAUER, P. W.; PAI, M. A. Power System Dynamics and Stability. Pretience Hall, Upper Saddle River, 1998.
7. KUNDUR, P. Power System Stability and Control. McGraw-Hill, New York, 1994.
8. DOMMEL, H. W.; SATO, N. Fast Transient Stability Solutions. IEEE Transactions on Power Aparatus and Systems, v. PAS-91, n. 4, jul 1972, p. 1643-1650. doi: https://doi.org/10.1109/TPAS.1972.293341