Mathematical Expression

The mathematical expression block uses the external library fparser and allows the user to insert generic mathematical expressions of any complexity combined with conditional structures in a control diagram, greatly increasing the program's generalization capability.

Syntax of mathematical expressions

The syntax of operations (for expressions A and B) are presented in the table below:

Operator	Expression
`( )`	Expression in parentheses first
`A unit`	A unit multiplier (if one has been added)
`A^B`	Exponentiation (`A` raised to the power `B`)
`-A`	Unary negation
`!A`	Unary logical negation (returns $1$ if `int(A)` is $0$ , otherwise $0$ )
`A*B` `A/B` `A%B`	Multiplication, division, and modulo
`A+B` `A-B`	Addition and subtraction
`A=B` `A<B` `A<=B` `A!=B` `A>B` `A>=B`	Comparison between `A` and `B` (returns $1$ or $0$ )
`A&B`	Returns $1$ if `int(A)` and `int(B)` are both nonzero, else $0$
`A\|B`	Returns $1$ if `int(A)` or `int(B)` is nonzero, else $0$

The mathematical functions supported by the library, which can be used in building block diagrams, are described in the table below:

Expression	Description
`abs(A)`	Absolute value of `A`. For real numbers, if `A` is negative, returns `–A`, otherwise returns `A`. For complex numbers the expression is equivalent to `hypot(real(x),imag(x))`.
`acos(A)`	Arccosine of `A`. Returns the angle in radians.
`acosh(A)`	Same as `acos()` but for hyperbolic cosine
`arg(A)`	Phase angle of a complex number `A`.
`asin(A)`	Arcsine of `A`. Returns the angle in radians.
`asinh(A)`	Same as `asin()`, but for hyperbolic sine
`atan(A)`	Arctangent of `A`. Returns the angle in radians.
`atan2(A,B)`	Arctangent of `A/B`, where the signs of both arguments determine the quadrant of the result. Returns the solution of the system: `hypot(A,B)sin(x)=A, hypot(A,B)cos(x)=B`. The returned value ranges from $-\pi$ to $\pi$ .
`atanh(A)`	Same as `atan()`, but for hyperbolic tangent.
`cbrt(A)`	Cube root of `A`.
`conj(A)`	Complex conjugate of `A`.
`ceil(A)`	Ceiling of `A`. Rounds up to the next highest integer.
`cos(A)`	Cosine of `A`. Returns the angle in radians.
`cosh(A)`	Same as `cos()`, but for hyperbolic cosine
`cot(A)`	Cotangent of `A`. Returns the angle in radians.
`csc(A)`	Cosecant of `A`. Returns the angle in radians.
`exp(A)`	Exponential of `A`. Returns e raised to the power of A.
`exp2(A)`	Exponential of `A` base 2.
`floor(A)`	Floor of `A`. Rounds down to the next lowest integer.
`hypot(A,B)`	Euclidean distance function.
`if(A,B,C)`	If `int(A)` is nonzero, returns `B`, else returns `C`.
`imag(A)`	Returns the imaginary part of complex number `A`.
`int(A)`	Rounds `A` to the nearest integer.
`log(A)`	Natural logarithm (base $e$ ) of `A`.
`log2(A)`	Base 2 logarithm of `A`.
`log10(A)`	Base 10 logarithm of `A`.
`max(A,B)`	If `A>B`, result is `A`, else `B`.
`min(A,B)`	If `A<B`, result is `A`, else `B`.
`polar(A,B)`	Returns the complex number with magnitude `A` and phase angle `B` (in radians).
`pow(A,B)`	Exponentiation (`A` raised to the power `B`)
`real(A,B)`	Returns the real part of complex number `A`.
`sec(A)`	Secant of `A`.
`sin(A)`	Sine of `A`. Returns the angle in radians.
`sinh(A)`	Same as `sin()`, but for hyperbolic sine.
`sqrt(A)`	Square root of `A`.
`tan(A)`	Tangent of `A`. Returns the angle in radians.
`tanh(A)`	Same as `tan()`, but for hyperbolic tangent.
`trunc(A)`	Truncated value of `A`. Returns the integer part of `A` without the fractional part.

It is possible to assign new variables using the following syntax:

<variable name> := <expression>; <function>

For example:

length := sqrt(x*x+y*y); 2*length*sin(length)

Tip

Spaces and newlines are ignored in expression parsing, so for better organization the previous code can be written as:

length := sqrt(x*x+y*y);
2*length*sin(length)

Warning

Note that the expression determining the block output value does not have a trailing ;.

Mathematical Expression Block Data Editing Form

The insertion and editing form for block inputs and the generic mathematical expression, as well as construction aid tools, is shown in the figure below.

In the “Input Variables” field a list of input names separated by spaces is entered. Any number of inputs can be defined in this list; these names are displayed on the graphical icon present in the control editor, as well as highlighted in the user-entered expression. The number of inputs and outputs behaves similarly to the sum blocks.

Below the input variables field there is a place for entering the mathematical expression. The syntax of the expression entered by the user has syntax highlighting (with different shapes and colors of the font) for numbers, operators, input variables, functions, and constants, facilitating creation, manipulation, and identification of typing and logic errors.

Information

As a user aid tool, expression verification was developed.

This tool will find errors and indicate to the user the type of error and its location, highlighting it. The previous figure exemplifies automatic error identification by PSP-UFU, as well as its position in the entered expression.

Mathematical Expression Example

The field current in $p.u.$ can be approximately estimated using the active power ( $P$ ) and reactive power ( $Q$ ), as well as the direct axis transient reactance ( $x_d$ ) and quadrature axis transient reactance ( $x_q$ ) and the terminal voltage magnitude ( $V$ ) of the machine:

i_f \approx \sqrt{ \left( V + Q' \right)^2 + P^2} + \left(\frac{x_d}{x_q} +1.0 \right) \times \frac{Q' \left( V + Q' \right) + {P'}^2}{\sqrt{\left( V + Q'\right)^2 + P^2}}

Where:

$P' = x_q \times \frac{P}{V}$
$Q' = x_q \times \frac{Q}{V}$

First, the quantities provided by PSP-UFU must be inserted in the "input variables" field. In this case, as can be seen in the input/output block, all necessary variables are provided: $P$ , $Q$ and $V$ . These variables must be inserted separated by spaces: p q v.

Using three input/output blocks, these data can be fed by connecting them to the mathematical expression block.

The direct axis transient reactance ( $x_d$ ) and quadrature axis transient reactance ( $x_q$ ) can be defined directly in the mathematical expression:

xd := 0.146;
xq := 0.0969;

The values of $P'$ and $Q'$ can also be calculated:

yp := xq * p / v;
yq := xq * q / v;

With all the necessary data, the field current can be calculated:

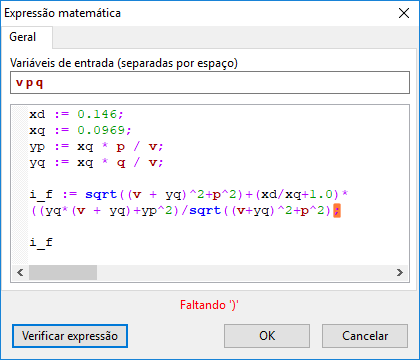
i_f := sqrt((v + yq)^2 + p^2) + (xd / xq + 1.0) *
       ((yq * (v + yq) + yp^2) / sqrt((v + yq)^2 + p^2));

Finally, the block output can be defined (without inserting ;):

i_f

Therefore, for inputs defined as p q v, the total mathematical expression for calculating the field current will be:

xd := 0.146;
xq := 0.0969;
yp := xq * p / v;
yq := xq * q / v;
i_f := sqrt((v + yq)^2 + p^2) + (xd / xq + 1.0) *
       ((yq * (v + yq) + yp^2) / sqrt((v + yq)^2 + p^2));
i_f

References

NIEMINEN, J.; YLILUOMA, J. Function Parser for C++ v4.5.2. Available at: <http://warp.povusers.org/FunctionParser/\>.

Syntax of mathematical expressions​

Mathematical Expression Block Data Editing Form​

Mathematical Expression Example​

References​

Syntax of mathematical expressions

Mathematical Expression Block Data Editing Form

Mathematical Expression Example

References