Transfer Function

The Transfer Function is an important elementary and essential block in a control system, as this component enables the representation of dynamic systems through algebraic equations in the frequency domain.

Information

In these blocks, the letter "s" is used for representation in the frequency domain, as this is the most commonly used terminology in control systems.

Transfer Function in PSP-UFU

After the transfer function is inserted, the program converts it into the state-space representation, since its solution is systematic, making it computationally more efficient.

Given a generic transfer function below:

$$\frac{Y(\bold{s})}{U(\bold{s})} = \frac{b_0 \bold{s}^k + b_1 \bold{s}^{k-1} + \cdots + b_{k-1} \bold{s} + b_k}{\bold{s}^k + a_1 \bold{s}^{k-1} + \cdots + a_{k-1} \bold{s} + a_k}$$

The transformation into state-space in the controllable canonical form is as follows:

$$\begin{bmatrix} \bold{s}x_1\\ \bold{s}x_2\\ \vdots\\ \bold{s}x_{k-1}\\ \bold{s}x_k \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_k & -a_{k-1} & -a_{k-2} & \cdots & -a_1 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_{k-1}\\ x_k \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix} u_n\\ y_n = \begin{bmatrix} \left( b_n - a_n b_0 \right) & \left( b_{n-1} - a_{n-1} b_0 \right) & \cdots & \left( b_1 - a_1 b_0 \right) \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_k \end{bmatrix} + b_0 u_n$$

The matrix differential equation is solved by the Implicit Trapezoidal method. An iterative process is performed until the error between calculations becomes less than a pre-established tolerance, and if the iterations become excessive, surpassing a maximum number defined by the user, the process is interrupted with an error. With the calculated state vector values ($x$), the output value of the block ($y_n$) is obtained.

Transfer Function Data Editing Form

The figure below shows the data editing form of the transfer function.

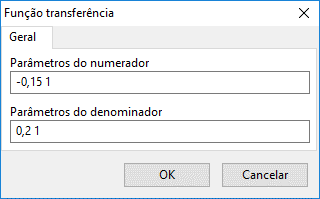
The transfer function is defined by the numerator and denominator coefficients, separated by spaces.

Caution!

Non-present elements are represented as coefficients with zero value.

For example, an entered parameter equal to “$\begin{matrix} 1 & 0.5 & 0 & 2 \end{matrix}$” will generate: “$s^3+0.5s^2+2$”.

References

1. OGATA, K. Modern Control Engineering. Prentice Hall Inc., New Jersey, 2004.