Função Transferência

A Função Transferência é um importante bloco elementar e essencial em um sistema de controle, visto que esse componente possibilita a representação de sistemas dinâmicos por meio de equações algébricas no domínio da frequência.

Informação

Nesses blocos é utilizado a letra “s” para representação no domínio da frequência, pois essa é a terminologia mais utilizada em sistemas de controle.

Função Transferência no PSP-UFU

Após a inserção da função transferência, o programa a transforma na representação em espaço de estado, visto que sua solução é sistemática tornando-a, assim, mais eficiente computacionalmente.

Dada uma função transferência genérica abaixo:

$$\frac{Y(\bold{s})}{U(\bold{s})} = \frac{b_0 \bold{s}^k + b_1 \bold{s}^{k-1} + \cdots + b_{k-1} \bold{s} + b_k}{\bold{s}^k + a_1 \bold{s}^{k-1} + \cdots + a_{k-1} \bold{s} + a_k}$$

A transformação em espaço de estado na forma canônica controlável ficará da seguinte forma:

$$\begin{bmatrix} \bold{s}x_1\\ \bold{s}x_2\\ \vdots\\ \bold{s}x_{k-1}\\ \bold{s}x_k \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_k & -a_{k-1} & -a_{k-2} & \cdots & -a_1 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_{k-1}\\ x_k \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix} u_n\\ y_n = \begin{bmatrix} \left( b_n - a_n b_0 \right) & \left( b_{n-1} - a_{n-1} b_0 \right) & \cdots & \left( b_1 - a_1 b_0 \right) \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_k \end{bmatrix} + b_0 u_n$$

A equação diferencial matricial é resolvida pelo método Trapezoidal Implícito. Um processo iterativo é realizado até que o erro entre os cálculos se torne menor que uma tolerância pré-estipulada e caso as iterações se tornem excessivas, ultrapassando um número máximo definido pelo usuário, o processo é interrompido com erro. Com os valores do vetor de estado ($x$) calculados obtém-se o valor da saída do bloco ($y_n$).

Formulário de edição de dados da Função Transferência

A figura abaixo apresenta o formulário de edição de dados da função transferência.

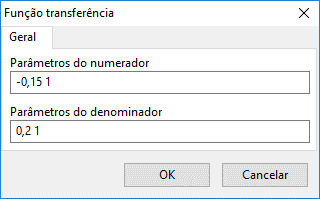
A função transferência é definida pelos coeficientes do numerador e denominador, separados por espaço.

Atenção!

Os elementos não presentes são representados como coeficientes de valor zero.

Por exemplo, um parâmetro inserido igual a “$\begin{matrix} 1 & 0{,}5 & 0 & 2 \end{matrix}$” irá gerar: “$s^3+0{,}5s^2+2$”.

Referências

1. OGATA, K. Modern Control Engineering. Prentice Hall Inc., New Jersey, 2004.